Spitzer & Saslaw Collision model
In a pioneering work about the collisional dynamics of dense
proto-galactic nuclei, Spitzer
& Saslaw (1966) introduced a simple, semi-analytical model to
determine the outcome (mass and energy loss) of high speed stellar
collisions. This approach has been applied by David, Durisen & Cohn (1987a,1987b)
and extended to unequal mass collisions by Sanders
(1970) and by Murphy,
Cohn & Durisen (1991).
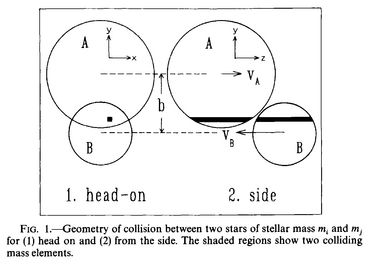Figure taken from Murphy, Cohn & Durisen (1991).
The computation preceeds as follows. The colliding stars are decomposed
into a lrage number of sticks, parallel to the direction of the relative
motion. It is assumed that, from the time of first contact, the
collision proceeds on a straight trajectory. In the overlapping regions
of the stars, one considers conservation of momentum and energy
(including thermal energy) in individual encounters between one stick
from the fisrt star and one stick from the other (in black on the
figure). No transverse energy or momentum transfer is taken into
account. If, after the collision, the total specific energy
of a stick relative to its parent star is higher than the binding
energy, G*M_star/R_star, this element of mass is considered lost from
the parent star (of mass M_star and radius R_star).
Although quite crude, this model gives results for the mass lost in
surprisingly good agreement with SPH simulations when the relative
velocity at infinity is larger than the stellar escape velocity and the
impact parameter is relatively large, d_min>0.4*(R_1+R_2).
Figure: comparison of the fractional mass loss between SPH simulations
by Freitag (Freitag 2000, Freitag & Benz
2002) and the Spitzer & Saslaw semi-analytical model applied to
the same stellar models.
This regime corresponds to most likely collisions in the centre-most
parts of a galactic nucleus where a central massive black hole imposes
high velocities. Future work, in particular detailed comparisons
with hydrodynamical simulations, will tell us if it can be used
to determine the entropy of gas elements in order to predict the
post-collisional stellar structure, in conjonction with some fluid
sorting algorithm, and if an extension of this method can be devised
for the regime of intermediate velocities (V_rel of order of V_star)
and/or small impact parameters.