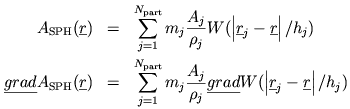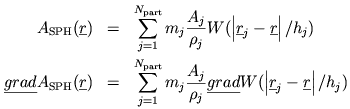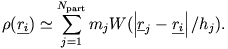Minimalist introduction to SPH

In Smoothed Particle Hydrodynamics, the fluid is represented as a set of N_part particles. The position of these particles are evolved according to equations of motion that incorporate gravitational and pressure forces. The particles are also given thermal energies which evolve adiabatically. Artificial viscosity terms are added to simulate shocks discontinuities.
Each particle is ascribed an interpolation kernel function W of spherical symmetry and variable size h (``smoothing length''). This allows the easy evaluation of fields and their derivatives. For instance, the iterpolated value of (scalar) field A and its gradient gradA at position r are given by:

where m_j, rho_j, and A_j are the mass, density and A values for particle j. In fact, the proper estimate of the density at the position of particle i is not but rho_j but

Hence particle i can be seen as a cloud spread inside a sphere of radius 2h_i. Only neighboring particles inside this sphere act on part. i with pressure forces. From the point of view of gravitation, SPH is completely similar to N-body approaches to which it borrows algorithms to compute gravitational forces more efficiently than the N_part² direct summation, for instance a binary tree (Press 1986, Benz et al. 1990).
When featured with a tree to compute gravitation, SPH is a grid-less method which can cope with any asymmetrical three dimensional geometry. It ignores void spaces completely, imposes no physical limits beyond which matter cannot be tracked, does not come into trouble with large dynamic range as long as variable smoothing lengths are implemented. In situations with highly anisotropic compressions, like the tidal interaction between a star and a massive black hole, SPH particles may, however, loose contact in directions of lowest compression. To cure this problem, SPH codes have been proposed that use ellipsoidal kernels (Fulbright et al. 95). The drawback of these schemes is that angular momentum is not exactly conserved anymore so they can only be applied in special cases where this will not endanger the physical significance of results. SPH is better suited to highly dynamical problems than to near-equilibrium configurations (Steinmetz & Mueller 93).