Monte Carlo code for stellar dynamics: Numerical implementation

As there exist various codes based on the pioneering ideas of Michel Hénon, each one with its pecularities, we concentrate here on Freitag's code while trying to concentrate on the features that are shared by all codes and to identify the differences between them.

Representation of the cluster

The MC code represents the cluster as a set of particles, each of which may be considered as a homogeneous spherical shell of stars sharing the same orbital and stellar properties. The number of particles may be lower than the number of stars in the simulated cluster but the number of stars per particle has to be the same for each particle.

Operation of the MC code

Here is a summary of how the Monte Carlo code operates:

How does the MC code work?

We won't cover the initialisation here, information may be found in (amongst others) Freitag & Benz 02 and Gürkan, Freitag & Rasio 04. Also check out the codes written by Atakan Gürkan (this link).
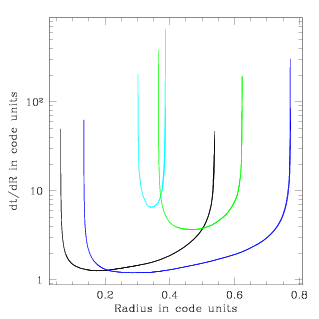
  1. Selection of a pair of neighbouring particles. Freitag's code keep Hénon's idea of time steps that are continuous function of the rank of the pair, i.e. its distance from the center. This allows to have a time step which follows the large variation of relaxation (and/or collision) time from the centre to the outskirts of the cluster
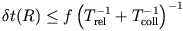
 delta t
where f is a small number (of order 0.01).
In the MIT/NU code, all particles share the same time step (a small fraction of the central relaxation time). So, in contrast to Freitag's code, all succesive pairs are selected and updated in turn before the potential is recomputed for the new configuration of particles. Giersz's approach is somewhat intermediate, with the particles being grouped into radial super-zones. All particles in a super-zone share the same time-step and can be modified at the same time (before potential is recomputed). Successive super-zones are defined so that the time step is multiplied by a factor of 2 from one super-zone to the next. Special care has to taken as to when super-zone crossing is allowed.
  1. Collisions. Physical collisions between single stars is implemented in Freitag's code. Interaction with binary stars (single-binary and binary-binary) is featured in Giersz and MIT/NU codes. For collisions, one computes the probability of stars from the neighbouring particles comming into contact during the time step:
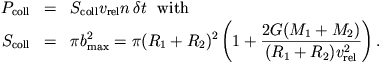
collision probability
Pcoll is compared to a [0,1[-random number. If this  number is smaller tan Pcoll, a collision occurs.  The impact parameter is selected randomly as b=bmax*sqrt(X) where X is another [0,1[-random number. The outcome of the collision can be, for instance, determined by interpolation into a table of pre-calculated SPH simulations (see the MODEST site on stellar collisions). In the case of interaction with binaries,  R1+R2 is replaced by (some factor times) the binary(ies) semi-major axis. In modern MC codes, the outcome is given through direct integration of the 3- or 4-body problem. Large-angle scatterings, not accounted for in the diffusive treatment of relaxation, can be included in a way similar to collisions, with
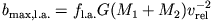
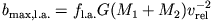
bmax large angle scattering
with fl.a. of order a few to include all events that lead to relatively large deflection angle.
  1. Super-encounter. The cumulative effect of all encounters between stars with the properties (and relative velocity) of the paire during the time step is reproduced, statistically, by a single 2-body encounter with deflection angle θSE proportional to the square root of the time step (see the physical principles). The time step has to be kept small enough for most of these super-encounter to have relatively small θSE. Indeed, in order to get the proper effect of relaxation, averaged over all possible position on a given orbit, relative velocities and mass of the second star, one need to realise a large number of super-encounter before the orbital properties are significantly changed.
  1. Modification of the orbit. The velocity has been slightly changed. This correspond to a small change of the orbital constant.
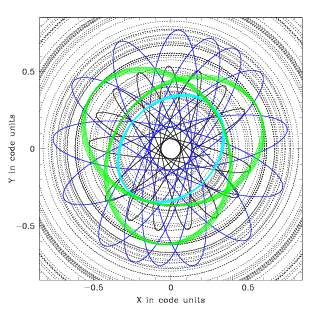
  1. New position on the orbit. A new position, i.e. a new radius for the shell is selected at random acccording to the time spent at each position. In the smooth, spherical potential defined by the collection of shells, orbits are rosettes. The time spent at a given distance exhibits divergences at the peri- and apo-centres. Implmenting such a probability density is a bit tricky, see Hénon 71a or Freitag & Benz 01.
orbits   orbital densities 
Note that, unlike in N-body codes, the change of position are discontinuous. If its eccentricity is large, a particle can jump over a range of radius representing a significant fraction of the cluster size in just one time step.
In Freitag's code, the potential is update after a particle has been moved around. An efficient way to do this is based on a binary tree structure.

Back to Monte Carlo home page